The APPROX_MEDIAN Function – A Test Case

The aim of this post is not to explain how the APPROX_MEDIAN function works (you find basic information in the documentation) but to show you the results of a test case I ran to assess how well it works.

Here’s what I did…

I started in the Oracle Database Public Cloud an instance of version 12.2.

Then I created a table with several numerical columns (the name of each column shows how many distinct values it contains), loaded 150 million rows into it (the size of the segment is 20 GB), and gathered the object statistics.

CREATE TABLE t AS
WITH
  t1000 AS (SELECT /*+ materialize */ rownum AS n
            FROM dual
            CONNECT BY level <= 1E3)
SELECT /*+ monitor */ rownum AS id,
       MOD(rownum,2) AS n_2,
       MOD(rownum,4) AS n_4,
       MOD(rownum,8) AS n_8,
       MOD(rownum,16) AS n_16,
       MOD(rownum,32) AS n_32,
       MOD(rownum,64) AS n_64,
       MOD(rownum,128) AS n_128,
       MOD(rownum,256) AS n_256,
       MOD(rownum,512) AS n_512,
       MOD(rownum,1024) AS n_1024,
       MOD(rownum,2048) AS n_2048,
       MOD(rownum,4096) AS n_4096,
       MOD(rownum,8192) AS n_8192,
       MOD(rownum,16384) AS n_16384,
       MOD(rownum,32768) AS n_32768,
       MOD(rownum,65536) AS n_65536,
       MOD(rownum,131072) AS n_131072,
       MOD(rownum,262144) AS n_262144,
       MOD(rownum,524288) AS n_524288,
       MOD(rownum,1048576) AS n_1048576,
       MOD(rownum,2097152) AS n_2097152,
       MOD(rownum,4194304) AS n_4194304,
       MOD(rownum,8388608) AS n_8388608,
       MOD(rownum,16777216) AS n_16777216,
       MOD(rownum,33554432) AS n_33554432,
       MOD(rownum,67108864) AS n_67108864,
       MOD(rownum,134217728) AS n_134217728
FROM t1000, t1000, t1000
WHERE rownum <= 150E6;
 
EXECUTE dbms_stats.gather_table_stats(USER,'t')

Once the test table was ready, I ran four queries for every column and measured the elapsed time, the maximum amount of PGA used by the query, and the precision of the result. Note that the test case was designed to avoid disk I/O operations. The buffer cache was large enough to store the whole test table and enough PGA was available to run the MEDIAN/APPROX_MEDIAN functions without having to spill data to a temporary tablespace. As a result, the processing was CPU bound. Also note that no parallel execution was used.

The following are the four test queries:

• The “regular” query using the MEDIAN function

SELECT median(n_m)
FROM t

• The MEDIAN function is replaced by the APPROX_MEDIAN function (non-deterministic processing)

SELECT approx_median(n_m)
FROM t

• The MEDIAN function is replaced by the APPROX_MEDIAN function (deterministic processing)

SELECT approx_median(n_m DETERMINISTIC)
FROM t

• Same approximate query as the previous one with, in addition, information about the error rate and its confidence

SELECT approx_median(n_m DETERMINISTIC),
       approx_median(n_m DETERMINISTIC, 'ERROR_RATE'),
       approx_median(n_m DETERMINISTIC, 'CONFIDENCE')
FROM t

Let’s have a look to three charts summarizing how well the APPROX_MEDIAN function works:

• The first chart shows that for both functions the elapsed time depends on the number of distinct values. That said, while for the non-deterministic processing with the APPROX_MEDIAN function the impact of the number of distinct values is minimal (the elapsed time goes between 24 and 33 seconds), for the deterministic processing with the APPROX_MEDIAN function and for the MEDIAN function it’s much higher (for the former, the elapsed time goes between 25 and 81 seconds; for the latter, the elapsed time goes between 97 and 182 seconds). Notice that I run the test a number of times and every time I got exactly the same results.

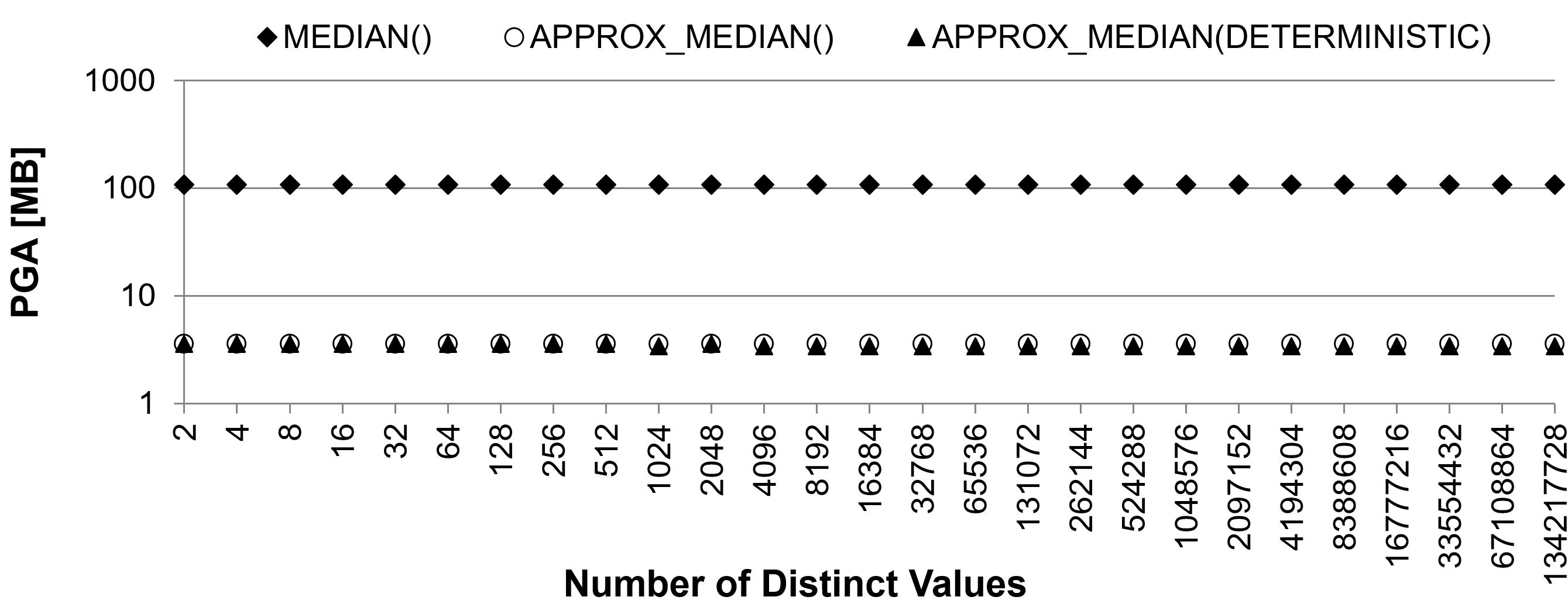
• The second chart (be careful that the y-axis scale is logarithmic) shows that for both functions the maximum amount of PGA doesn’t depend on the number of distinct values. It is about 100MB for the MEDIAN function, and about 4MB for the APPROX_MEDIAN function.

• The aim of the third chart is threefold. First, it shows that the precision of the APPROX_MEDIAN function is better when it performs a deterministic processing. Second, that the precision of the APPROX_MEDIAN function is decent only when there are at least a dozen of distinct keys. Third, that the error rate returned by the APPROX_MEDIAN function isn’t very reliable (note that for all values a confidence of 99% was given).

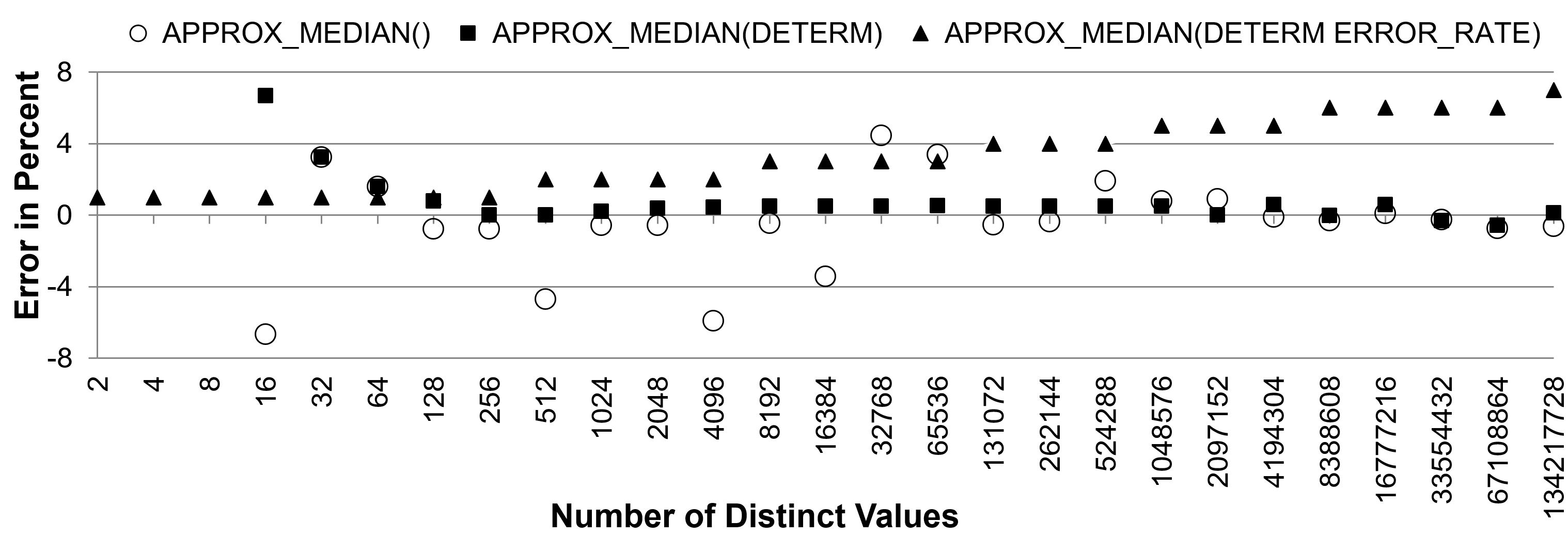
According to this test case, in my opinion, the performance and accuracy of the APPROX_MEDIAN function with numerical values (I still have to test other data types), provided that the number of distinct value isn’t too low, are good. Only the error rate and confidence information aren’t very reliable. It goes without saying that it would be interesting to run a similar test with different values/distributions to see whether the results would change.